Mathematics is a field that has intrigued and fascinated humanity for centuries. From its humble beginnings in ancient civilizations to its pervasive influence in modern science and technology, mathematics has played a fundamental role in shaping our understanding of the world.
The extent of mathematical discovery and application seems, as never before, to be boundless. Yet, surprisingly, few people understand the real nature and purpose of mathematics. Many look upon mathematics as just a study of various numbers and an attempt to skillfully perform endless calculations. Some envision mathematics as an envious conglomerate of strange symbols and peculiar-looking equations. Others view the mighty machines of today as the epitome of mathematical prowess. Mathematics is none of these, although each one of them is used by mathematicians.
In this comprehensive blog post, we will delve into the nature of mathematics, exploring its foundational principles, its applications across various disciplines, its abstract and universal nature, and its role in fostering creativity and innovation.
Foundational Principles of Mathematics
Mathematics is a realm of abstract concepts and logical reasoning that underpins nearly every aspect of our lives. From the simple act of counting to the complex algorithms powering our digital world, mathematics forms the bedrock upon which our understanding of the world rests. At the heart of this vast and intricate discipline lie its foundational principles, which provide the framework for mathematical reasoning and discovery.
Although the substance of mathematics fills volumes and can be very difficult, there are some basic fundamental concepts underlying the very heart of the subject that almost everyone can understand. Understanding these will add measurably to ones vision and appreciation of mathematics. These concepts will also provide a suitable beginning from which we may move more naturally into the main body of the subject.
Below are some of the fundamental principles of Mathematics
1. Axioms: The Building Blocks of Mathematics
At the core of mathematics lie axioms, which are fundamental truths accepted without proof. These axioms serve as the starting point for mathematical reasoning, providing a set of rules upon which the entire mathematical edifice is constructed.
Join my newsletter in order to gain access to cutting-edge research and developments along with free revision guides and exercises.
Axioms are self-evident truths that are assumed to be true without the need for demonstration. For example, in Euclidean geometry, one of the most well-known sets of axioms is Euclid’s postulates, which include statements such as “Two points determine a unique line” and “A straight line can be extended indefinitely in both directions.”
2. Theorems: Deductive Reasoning and Logical Inference
From these axioms, mathematicians derive theorems, which are statements that can be proven using logical deduction. The process of proving a theorem involves applying the rules of logic to the axioms to establish the truth of the statement.
This process of deductive reasoning forms the backbone of mathematical proof, ensuring that mathematical conclusions are derived logically from a set of accepted premises. Theorems serve as the building blocks of mathematical knowledge, providing a framework for understanding and extending mathematical concepts.
3. Rigorous Reasoning: Precision and Clarity
One of the hallmarks of mathematics is its emphasis on rigorous reasoning and precision. Mathematical arguments must be clear, logical, and free from ambiguity to be considered valid. Mathematicians employ a variety of techniques to ensure the rigor of their proofs, including deductive reasoning, induction, and contradiction.
These techniques allow mathematicians to construct watertight arguments that establish the truth of mathematical statements beyond any doubt. Rigorous reasoning is essential not only for proving theorems but also for formulating conjectures, defining new concepts, and exploring the boundaries of mathematical knowledge.
3. Abstract Structures: Beyond the Physical World
While many mathematical concepts have clear real-world applications, much of mathematics deals with abstract structures and relationships that may not have an immediate physical interpretation. From the algebraic structures of groups, rings, and fields to the topological spaces of topology, mathematics abounds with abstract entities that exist purely in the realm of ideas.
These abstract structures often provide powerful tools for understanding and solving real-world problems, transcending the limitations of physical intuition and observation. Mathematicians study these abstract structures for their intrinsic properties, exploring the deep connections and patterns that underlie the fabric of mathematical reality.
Applications of Mathematics
Mathematics is not just a theoretical pursuit confined to the realms of academia. Rather, it is a powerful tool with myriad practical applications that permeate almost every aspect of our lives. From the design of buildings and bridges to the algorithms powering our digital devices, mathematics plays a crucial role in shaping our modern world.
I have enumerated some of the diverse and fascinating applications of mathematics across various domains.
1. Mathematics in Science
Science and mathematics have always been closely intertwined, with mathematical principles providing the language and framework for understanding the natural world. In physics, mathematics is essential for describing the laws of motion, the behavior of waves and particles, and the structure of the universe. From the elegant equations of classical mechanics formulated by Newton to the mind-bending concepts of relativity and quantum mechanics developed by Einstein and others, mathematics lies at the heart of our understanding of the cosmos.
In biology, mathematics is used to model the dynamics of ecosystems, analyze genetic sequences, and understand the complex interactions between organisms. Mathematical techniques such as differential equations, probability theory, and network theory provide powerful tools for studying biological systems at various scales, from the molecular level to the population level.
In chemistry, mathematics is indispensable for modeling chemical reactions, predicting molecular structures, and understanding the properties of materials. Mathematical concepts such as calculus, linear algebra, and computational methods are used to solve complex problems in chemical kinetics, thermodynamics, and quantum chemistry.
2. Mathematics in Engineering
Engineering is another field where mathematics plays a central role, providing the analytical tools and techniques needed to design, analyze, and optimize systems and structures. In civil engineering, mathematics is used to calculate loads and stresses in buildings and bridges, design efficient transportation networks, and model the behavior of fluids and materials.
In mechanical engineering, mathematics is essential for designing machines and mechanical systems, analyzing the forces and motions of objects, and optimizing the performance of engines and turbines. Mathematical concepts such as calculus, differential equations, and numerical methods are used to solve problems in fluid dynamics, heat transfer, and structural analysis.
In electrical engineering, mathematics is used to design circuits and electronic devices, analyze signals and systems, and develop algorithms for communication and control. Mathematical techniques such as Fourier analysis, linear algebra, and probability theory are used to analyze and manipulate signals and data in various applications, from wireless communication to digital signal processing.
3. Mathematics in Technology
Technology is another area where mathematics plays a crucial role, driving innovations in fields such as computer science, telecommunications, and information technology. In computer science, mathematics is used to develop algorithms and data structures, analyze the efficiency and complexity of algorithms, and design cryptographic protocols and security systems.
Join my newsletter in order to gain access to cutting-edge research and developments along with free revision guides and exercises.
In telecommunications, mathematics is used to model and optimize communication networks, analyze the performance of wireless systems, and develop coding and modulation schemes for reliable data transmission. Mathematical concepts such as graph theory, information theory, and coding theory are used to design and analyze communication systems and protocols.
In information technology, mathematics is used to develop encryption algorithms, analyze and manipulate data, and design algorithms for artificial intelligence and machine learning. Mathematical techniques such as linear algebra, probability theory, and optimization methods are used to solve problems in data analysis, pattern recognition, and decision making.
The Abstract and Universal Nature of Mathematics
Mathematics transcends cultural boundaries and defies the constraints of time and space, revealing profound truths about the nature of reality.
Let us now explore a few of its far-reaching implications.
1. Abstract Reasoning: Beyond the Tangible
At its core, mathematics is a realm of abstract reasoning, where concepts and structures exist purely as mathematical abstractions, divorced from any physical interpretation. From the complex algebraic structures of groups and rings to the geometric spaces of topology, mathematics abounds with abstract entities that exist solely in the realm of ideas.
These abstract concepts serve as the building blocks of mathematical knowledge, providing a framework for exploring the deep connections and patterns that underlie the fabric of mathematical reality.
One of the most remarkable aspects of mathematics is its ability to describe and analyze phenomena that may not have a direct physical interpretation. For example, in abstract algebra, mathematicians study groups, which are sets equipped with operations that satisfy certain properties. While the elements of a group may represent tangible objects or transformations in the physical world, the structure of the group itself is an abstract mathematical concept that transcends any specific instantiation.
3. Universality of Mathematical Truths: A Common Language for Understanding the World
Despite its abstract nature, mathematics possesses a remarkable universality, with its laws and principles applying equally well in different contexts and cultures. Mathematical truths are independent of human beliefs or opinions, providing a common language for expressing and analyzing natural phenomena.
Whether describing the motion of celestial bodies, the behavior of financial markets, or the structure of molecules, mathematics provides a universal framework for understanding the underlying patterns and relationships that govern the world around us.
One of the key features of mathematics is its ability to uncover deep connections and symmetries that exist across seemingly disparate domains. For example, the concept of symmetry plays a central role in various branches of mathematics, from algebra and geometry to physics and chemistry. Symmetry is a universal principle that underlies the structure of crystals, the laws of conservation in physics, and the patterns of beauty in art and nature. By studying these symmetries, mathematicians gain insights into the underlying order and harmony of the universe, revealing hidden patterns and relationships that lie beneath the surface of reality.
4. Mathematical Beauty: The Elegance of Pure Reason
Beyond its practical applications and universal truths, mathematics possesses a profound aesthetic beauty that captivates the imagination and inspires awe and wonder. Mathematicians often describe their work as a blend of art and science, where creativity and intuition play as significant a role as logic and reasoning. The beauty of mathematics lies in its elegance and simplicity, with elegant proofs and structures that reveal the underlying harmony and order of the mathematical universe.
To the ancient scientists, numbers meant whole numbers and for Pythagoras, to prove the point that everything in the universe was Number, you had to give him two numbers x and y and he would promptly produce a third number z such that

When confronted with the problem of whether or not there exist integers x, y, and z such that
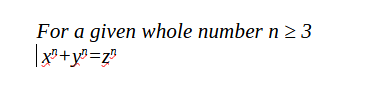
which has no immediate solution over the integers, the ancient mathematicians said that any such any such triple x, y and z are no numbers. It took mathematicians over 2500 years to resolve the problem.
As far as the famous mathematician Leopold Kroneeker (1823-1891) was concerned, God himself made the whole numbers: anything else is the work of man. The very concept of numbers proceeding to infinity, in any direction, appeared only in the imagination of theologians and the greatest astronomers and mathematicians, such as Archimedes, who exhausted a circle with indefinitely many polygons in his attempt to calculate the number of grains of sand required to fill the universe. What is most important to us today is to be able to use numbers and abstract symbols to attempt to make forecast of things that are predictable. One famous scientist once said
Mathematics and Creativity
Mathematics isn’t just about solving problems or crunching numbers; it’s also a playground for creativity. Many people don’t realize how much creativity is involved in math. So, we’ll explore how mathematics and creativity go hand in hand, showing how they work together to solve problems and make new discoveries.
Problem-Solving with a Twist
Mathematics is all about solving problems, but it’s not always a straightforward process. Sometimes, the usual methods don’t work, and that’s where creativity comes in. Mathematicians have to think outside the box, coming up with new ways to tackle tough problems. It’s like a puzzle where you have to find different ways to fit the pieces together.
Thinking Outside the Lines
Math isn’t just about numbers; it’s also about patterns and shapes. Mathematicians use their creativity to see connections between different ideas and to visualize complex concepts. They might use diagrams or drawings to help them understand a problem better. Creativity allows them to explore new avenues and come up with innovative solutions.
Playing with Numbers
Numbers might seem boring, but they can be pretty fascinating when you look at them in the right way. Mathematicians use their creativity to find interesting patterns and relationships between numbers. They might discover sequences or formulas that nobody has ever seen before. It’s like discovering a hidden treasure in a sea of numbers.
Exploring New Frontiers
Mathematics is always evolving, with new discoveries being made all the time. Mathematicians are like explorers, venturing into uncharted territory to uncover new truths. Creativity fuels their journey, helping them to see things in new ways and make connections that others might miss. It’s a never-ending quest for knowledge and understanding.
Today, mathematics is one of the fastest growing and the most radically changing sciences. Although new discoveries often render former theories obsolete in many scientific disciplines, nearly all the major mathematical discoveries of the past 4000 – 5000 years are still useful and valid.
Conclusion
Mathematics, despite its awesome reputation, is the simplest and clearest of studies dealing with laws of thought and reasoning. We are all mathematicians of sort! How often, when in a conversation with another person, do we find ourselves asserting that such and such is true, then following that assertion with a sequence of facts, each designed to help establish or prove our point? Proclaiming something true or valid under certain conditions, then proceeding to gather supporting facts and presenting them in an orderly, logical manner, is probably, the most fundamental characteristic of mathematics.
Throughout history, man has always welcomed and even sought out the kinds of problems that would challenge his keenest insight and produce clever facts of ingenuity. Mathematics, in its simplest form, deals with reasoning and the laws of thought, which are usually devoted to the proof of an assertion or to the solution of a problem. This thinking process often takes place without the use of numbers and excessive calculations.
Join my newsletter in order to gain access to cutting-edge research and developments along with free revision guides and exercises.
Mathematics is neither a hard science nor an art, which delights the major part of the public. However, mathematics is usually explained and justified to the world at large by giving examples of important inventions that would not have been made without its help. This explanation is embodied in the myth that mathematicians concern themselves with external truths which they hand down to physicists, who pass them down to chemists and engineers, etc, who, eventually, pass them on to mankind as a whole. Though there are examples (very important ones indeed) that pass along the chain in both ways, it is also important to note that it is a narrow view to isolate mathematicians on such a pedestal. There is a more socially grounded view which says that mathematics and mathematicians are deeply embedded in the human culture and are tied to the arts in particular, where the love for abstraction flourishes.
Mathematics touches every sector of our lives; from the small-scale dealer by the roadside through the shop assistant and the classroom teacher to the politician (in any order). There comes a time when a member from each class of the society is faced with the need to optimize the resources that the classes have at their disposal. How such a situation is handled would depend on how the decision maker handles his/her figures.
What must we do to love mathematics? Passion for the subject can be a starting point, though a mere realization of the important fact, that lacking numeracy skills narrows one’s choices for future employment may be a sufficient booster.
While it is acceptable, in the name of freedom of choice and will, to think that mathematics is dreadful, difficult to learn and boring, it must be pointed out that it is not the main task of a school, college or university to provide amusement to pupils or students. Real learning may also be strenuous.
Mathematicians have an educational stewardship responsibility, which is primary to post-secondary mathematics education, as well as an important responsibility in the training of mathematics teachers.
It took a long time to achieve widespread reading literacy in the world, and it will take long to achieve a widespread mathematical literacy.
Tondeur
Being mathematically literate is a situation that cannot be avoided, given that the foreseeable future is going to be one of unprecedented pervasiveness of mathematical thought through out the sciences. In a data driven world, mathematical concepts and algorithmic processes will be the primary navigational tools. In this connection, a country that must survive the global race for knowledge and its uses needs mathematics of scientifically high quality and a mathematically well-educated public.
Join my newsletter in order to gain access to cutting-edge research and developments along with free revision guides and exercises.
There is therefore a need to:
- Redefine the curriculum
- Change and revamp the education of teachers
- Reach standards of quality control that secure a uniformly high level of mathematics and mathematical education, across all levels of our educational system.
- Institute incentives that would encourage mathematical training at all levels
- Achieve enjoyment of mathematics by simplifying its presentation and making it available to the larger community at an affordable price.
It is my aim to offer a rendition of the common concepts that are important in understanding the very foundations of mathematical analysis.
